Задача 2
Имеются данные о заработной плате работников предприятия за два года:
|
Цех |
Базисный год |
Отчётный год | ||
|
Средняя з/п 1 работника за месяц, руб. |
Среднее списочное число работников, ч. |
Средняя з/п 1 работника за месяц, руб. |
Фонд з/п тыс. руб. | |
|
1 |
5800 |
100 |
6200 |
682000 |
|
2 |
6500 |
150 |
6800 |
952000 |
Определить:
Среднемесячную заработную плату работника за каждый год и её изменение (в сумме и %);
Указать виды средних.
Решение:
. Определим среднее списочное число работников за отчётный год:
Среднее списочное число = Фонд заработной платы / средняя заработная плата 1 раб за месяц.
Чтобы найти среднее списочное число работников за отчётный год нужно фонд заработной платы 1 и 2 цехов поделить на среднюю заработную плату работника за месяц, за отчётный год.
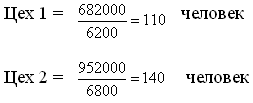
Для определения среднемесячной зарплаты работника за год воспользуемся формулой средней арифметической взвешенной.
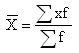
Чтобы найти среднемесячную зарплату работника за базисный год нужно:
Базисный год = S средняя зарплата работника за месяц цех 1 * среднесписочное число работников цех 1 + S средняя зарплата работника за месяц цех 2 * среднее списочное число работников цех 2 / S среднее списочное число работников - ![]()
среднемесячная зарплата работника за базисный год.
Чтобы найти среднемесячную зарплату работника за отчётный год нужно:
Отчётный год = S средняя зарплата работника за месяц цех 1 * среднесписочное число работников цех 1 + S средняя зарплата работника за месяц цех 2 * среднее списочное число работников цех 2 / S среднее списочное число работников - 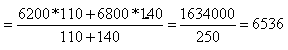
среднемесячная зарплата работника за отчётный год.
Изменение средней зарплаты работника за каждый год в сумме =
= 6536-6220=316 руб.
Изменение средней зарплаты работника за каждый год в % =
= ![]()
. В статистике применяются различные виды средних: арифметическая, гармоническая, квадратическая, геометрическая, структурные средние - мода и медиана. Средние, кроме моды и медианы исчисляются в 2-х формах: простой и взвешенной.
В данной задаче используются арифметический вид средних взвешенной формы.
Задача 3
По данным микропереписи 1994г. получено следующее распределение населения, проживающего в месте постоянного жительства не с рождения.
|
Продолжительность проживания в месте постоянного жительства, лет |
Середина интервала |
Доля населения % |
Накопленные частоты |
|
Менее 2 |
1 |
7,5 |
7,5 |
|
2-5 |
3,5 |
11,0 |
18,5 |
|
6-9 |
7,5 |
10,5 |
29,0 |
|
10-14 |
12 |
12,3 |
41,3 |
|
15-24 |
19,5 |
21,1 |
62,4 |
|
25 и более |
29,5 |
37,6 |
100,0 |
|
Итого |
100 |
